LOGIC Functions

LOGIC Functions

1. Logic Variables

2. Logic Operations

3. The AND Function

4. The OR Function

5. The NOT Function

6. The NAND Function

7. The NOR Function

8. The Exclusive OR(X-OR) Function

9. The Exclusive NOR(X-OR) Function

10. Boolean Expressions

11. Truth Tables

12. Karnaugh Maps

Logic Variable

ตัวแปรทางลอจิกจะมีลักษณะของการทำงานอยู่ 2 แบบ คือ เปิด และ ปิด

Logic Operations

ปฏิบัติการพื้นฐานของพีชคณิตบูลีนมี อยู่ 3 แบบคือ

1. การ รวมทางลอจิก (Logic Addition) เรียก ว่า OR จะใช้เครื่องหมาย (+)

2. การ คูณทางลอจิก (Logic Multiplication) เรียกว่าการ AND จะใช้เครื่องหมาย (.)

3. การ คอมพลีเมนต์ทางลอจิกหรือการกลับค่า (Logic Complementation) จะใช้เครื่องหมาย (-) หรือเรียกว่า NOT หรือบางครั้งเรียกว่าเครื่องหมาย บาร์ (bar)

TOC

---

The AND Function

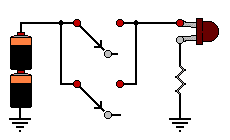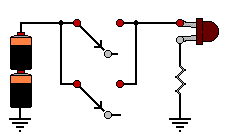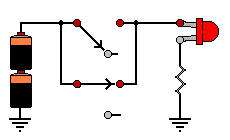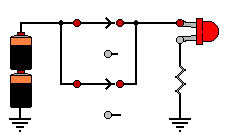
AND มีลักษณะการทำงานเหมือนกับวงจรไฟฟ้าที่สวิตช์ ต่อแบบอนุกรมกันอยู่ ดังรูป

ตารางความ จริง

INPUT

OUTPUT

A

B

Y

0

0

0

0

1

0

1

0

0

1

1

1

INPUT

สัญลักษณ์

ทฤษฎี

2

3

4

TOC

---

The OR Function

OR มีลักษณะการทำงานเหมือนกับวงจรไฟฟ้าที่สวิตช์ ต่อแบบขนาดกันอยู่ ดังรูป

ตารางความ จริง

INPUT

OUTPUT

A

B

Y

0

0

0

0

1

1

1

0

1

1

1

1

INPUT

สัญลักษณ์

ทฤษฎี

2

3

4

TOC

---

The NOT Function

ตารางความ จริง

INPUT

OUTPUT

A

Y

0

1

1

0

สัญลักษณ์ ลอจิก

ทฤษฎี

TOC

---

The NAND Function

ตารางความ จริง

INPUT

OUTPUT

A

B

Y

0

0

1

0

1

1

1

0

1

1

1

0

INPUT

สัญลักษณ์

ทฤษฎี

2

3

4

TOC

---

The NOR Function

ตารางความ จริง

INPUT

OUTPUT

A

B

Y

0

0

1

0

1

0

1

0

0

1

1

0

INPUT

สัญลักษณ์

ทฤษฎี

2

3

4

TOC

---

The Exclusive-OR (X-OR) Function

ตารางความ จริง

INPUT

OUTPUT

A

B

Y

0

0

1

0

1

0

1

0

0

1

1

1

สัญลักษณ์ ลอจิก

ทฤษฎี

หรือ

TOC

---

The Exclusive-NOR (X-NOR) Function

ตารางความ จริง

INPUT

OUTPUT

A

B

Y

0

0

0

0

1

1

1

0

1

1

1

0

สัญลักษณ์ ลอจิก

ทฤษฎี

หรือ

TOC

---

ตารางความ จริง(Truth Table)

ตารางความจริงประกอบด้วยอินพุทหรือเรียกว่า ตัวแปร (Variable) ซึ่ง มักจะมากกว่า 1 อินพุทและเอาท์พุทซึ่งจะมี 1 เอาท์พุท ตารางความจริงจะแสดงค่าระดับลอจิกด้านเอาท์พุทที่สัมพันธ์กันเงื่อนไขและการ จัดหมวดหมู่ของทางด้านอินพุท รูปแบบของตารางความจริงจะมีกี่แถวหรือบรรทัดนั้น ขึ้นอยู่กับจำนวนอินพุทหรือตัวแปร ซึ่งเป็นไปตามสูตร

จำนวนแถว(บรรทัด) =

n=จำนวนอินพุทหรือตัว แปร

ตาราง 2 ตัวแปร

จะได้ แถว

INPUT

OUTPUT

A

B

Y

0

0

x

0

1

x

1

0

x

1

1

x

ตาราง 3 ตัวแปร

จะได้ แถว

INPUT

OUTPUT

A

B

C

Y

0

0

0

x

0

0

1

x

0

1

0

x

0

1

1

x

1

0

0

x

1

0

1

x

1

1

0

x

1

1

1

x

สมการ Sum Of Product (SOP)

จะนำที่มีเอาต์พุทเป็น 1 มาพิจารณา และ เขียนเทอมของตัวแปร A,B,C ออกมาที่ละเทอม โดยแทนค่าตัวแปรที่เป็น 0 ด้วย และตัวแปรที่เป็น 1 จะแทนตัว A แต่ละตัวกระทำการด้วย AND และนำเทอมที่ เขียนได้จากเอาต์พุทที่เป็น 1 ทั้งหมดมากระทำการ OR กัน ซึ่งเรียกว่า Sum Of Product หรือ สมการแบบ Min term

ตาราง 3 ตัวแปร

จะได้ แถว

INPUT

OUTPUT

A

B

C

Y

0

0

0

0

0

1

0

1

0

0

1

1

1

0

0

1

0

1

1

1

0

1

1

1

ตัวอย่างที่ 1 Y(A,B,C)=(1,2,5,6,7)

ตัวอย่างที่ 2 Y(A,B,C)=(0,1,6,7)

ตัวอย่างที่ 3 Y(A,B,C,D)=(0,1,2,3,5,6,7,12,13)

ตัวอย่างที่ 4 Y(A,B,C,D)=(6,7,8,9,13,14,15)

สมการ Product Of Sum (POS)

จะนำที่มีเอาต์พุทเป็น 0 มาพิจารณา และ เขียนเทอมของตัวแปร A,B,C ออกมาที่ละเทอม โดยแทนค่าตัวแปรที่เป็น 0 ด้วย A และตัวแปรที่เป็น 1 จะแทนด้วย แต่ละตัวกระทำการด้วย OR และนำเทอมที่ เขียนได้จากเอาต์พุทที่เป็น 1 ทั้งหมดมากระทำการ AND กัน ซึ่งเรียกว่า Product Of Sum หรือ สมการแบบ Max Term

TOC

---

ทฤษฎีบูลีน(Boolean Expression)

ความรู้ เบื้องต้น

ทฤษฏีพีชคณิตของบูลีน(boolean)

T1: กฏการสลับ ที่ (commutative law)

(a) A+B = B+A

(b) A.B = B.A

T2: กฏความ สัมพันธ์ (associative law)

(a) (A+B)+C = A+(B+C)

(b) (A.B).C = A.(B.C)

T3: กฏการกระจาย(distributive law)

(a) A.(B+C) = A.B + A.C

(b) A+(B.C) = (A+B).(A+C)

T4: กฏของ เอกลักษณ์ (indentity law)

(a) A+A = A

(b) A.A = A

T5:

(a)

(b)

T6:

(a) A + A B = A

(b) A ( A + B ) = A

T7:

(a) 0 + A = A

(b) 0 A=0

T8:

(a) 1+ A = 1

(b) 1 A = A

T9:

(a)

(b)

T10:

(a)

(b)

T11: De Morgan's Theorem

(a)

(b)

---

Examples

Prove T10 : (a)

(1) ใช้ Algebra มีวิธีทำ ดังนี้

(2) ใช้ตารางความจริง มีวิธีทำดังนี้

จากกฏที่ให้ข้างบนเราสามารถ ใช้กฏการซ้ำซ้อนกันมาแก้ปัญหาได้ดังนี้

---

แบบฝึกหัด

(a) จงแสดงวิธีการแก้ปัญหากฏข้อ ที่ 10

(b) จากตารางที่กำหนดให้แสดงการแก้ปัญหาโดยใช้กฏข้อที่ T11 (a) และ (b)

Clickดูคำตอบ

TOC

---

Karnaugh Maps

การลดรูปสมการลอจิก โดยการใช้พีชคณิตบูลีนหรือ ทฤษฎีของ De Morgan ที่ผ่านมายังมีความยุ่งยากซับซ้อน แต่เรามีวิธีการที่จะทำให้สมการบูลีนสั้นและง่ายที่สุดอย่างรวดเร็วโดยใช้ แผนผังคาร์นอร์ (Karnaugh Map) ซึ่งผังคาร์นอร์นี้จะเป็นพื้นผิวทรง กลม แต่การพิจารณาไม่สามารถเขียนเป็นลักษณะทรงกลมได้จึงต้องทำในลักษณะของรูปสี่ เหลี่ยมผืนผ้าดังรูปที่เห็นทั่วไป แผนผังคาร์นอร์อาจใช้ได้สูงถึง 6 ตัวแปร แต่ในครั้งนี้จะใช้เพียง 2,3 และ 4 ตัวแปรเท่านั้น

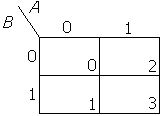
ผังคาร์นอร์ 2 ตัวแปร

ขั้นตอนมี ดังนี้

1. นำ เอาสมการ f(A,B) =(1,2,3) แทนลงในผังคาร์นอร์ โดยแทนตัวเลข 1 ลงในช่อง 1,2 และ 3 ตามลำดับ ดังรูป

2. ทำ การรวมโดยรวมช่องที่ติดกันเข้าด้วยกัน โดยมีหลักดังนี้

o รวม ในแนวนอน

o รวม ในแนวตั้ง

o สามารถ รวมซ้ำได้อีกถ้าต้องการ โดยจะต้องไม่เป็นไปในลักษณะของวงกลม

o การ รวมจะอยู่รูปของ นั้นคือ (1,2,4,8...)

3. นำ ผลที่ได้มาทำการ OR กัน ก็จะเป็นคำตอบของสมการบูลีนที่ลดรูปแล้ว

จะพบว่าผังคาร์นอร์ 2 ตัวแปรนั้นจะไม่ค่อยได้นำไปใช้งานมากนัก เพราะว่ากรณี 2 ตัวแปร ก็จะอยู่ในรูปของเกตพื้นฐาน ทั้ง 7 ชนิดนั้นเอง

ตัวอย่างที่ 5
ตัวอย่างที่ 6
TOC

ผังคาร์นอร์ 3 ตัวแปร

ผังคาร์นอร์ 3 ตัวแปรก็จะมีขั้นตอนเหมือนกับ 2 ตัวแปร แต่จะมีขนาดของตารางที่ใหญ่ขึ้น เป็นขนาด 4x2 ช่อง

แบบแนวตั้ง

แนวนอน

Animation(shockwave)

ตัวอย่างที่ 7 f(ABC)=(0,2,5,7)
ตัวอย่างที่ 8 f(ABC)=(2,3,4,5)
ตัวอย่างที่ 9 f(ABC)=(0,1,4,5)
ตัวอย่างที่ 10 f(ABC)=(0,5)
ตัวอย่างที่ 11 f(ABC)=(1,5)
ตัวอย่างที่ 12 f(ABC)=(2,3,6,7)
ตัวอย่างที่ 13 f(ABC)=(1,3,5,7)

TOC

ผังคาร์นอร์ 4 ตัวแปร

ผังคาร์นอร์ 4 ตัวแปรก็จะมีขั้นตอนเหมือนกับ 2 ตัวแปร แต่จะมีขนาดของตารางที่ใหญ่ขึ้น เป็นขนาด 4x4 ช่อง ดังรูป

ตัวอย่างที่ 14f(ABCD)=(0,1,7,8,10)
ตัวอย่างที่ 15f(ABCD)=(2,4,6,712,13,15)
ตัวอย่างที่ 16f(ABCD)=(1,5,7,10,13,14,15)
ตัวอย่างที่ 17f(ABCD)=(4,6,8,9,10)
ตัวอย่างที่ 18f(ABCD)=(0,2,8,10)
ตัวอย่างที่ 19f(ABCD)=(0,1,2,3,8,9,10,11)

ตัวอย่างที่ 1

f(A,B,C)=(1,2,5,6,7) แปลงเป็นตารางจะได้ดังนี้

INPUT

OUTPUT

SOP

A

B

C

Y

0

0

0

0

-

0

0

1

1

0

1

0

1

0

1

1

0

-

1

0

0

0

-

1

0

1

1

1

1

0

1

1

1

1

1

จากนั้นนำทั้ง 5 เทอมมาทำการ OR กัน ก็จะได้ฟังก์ชันแบบ SOP ดังนี้

คลิกที่นี่ดูวงจร

จากนั้นทำการลดรูป ฟังก์ชันได้ดังนี้ คลิกที่นี้ดูการลดรูป

จะได้คำตอบดังนี้ คลิกที่นี่ดูวงจร

---

กลับ

ตัวอย่าง ที่ 2

f(A,B,C)=(0,1,6,7) แปลงเป็นตารางจะได้ดังนี้

INPUT

OUTPUT

SOP

A

B

C

Y

0

0

0

1

0

0

1

1

0

1

0

0

-

0

1

1

0

-

1

0

0

0

-

1

0

1

0

-

1

1

0

1

1

1

1

1

จากนั้นนำทั้ง 4 เทอมมาทำการ OR กัน ก็จะได้ฟังก์ชันแบบ SOP ดังนี้

คลิกที่นี่ดูวงจร

จากนั้นทำการลดรูป ฟังก์ชันได้ดังนี้ คลิกที่นี้ดูการลดรูป

จะได้คำตอบดังนี้ คลิกที่นี่ดูวงจร

---

กลับ

ตัวอย่าง ที่ 3

Y(A,B,C,D)=(0,1,2,3,5,6,7,12,13) แปลงเป็นตารางจะได้ดังนี้

INPUT

OUTPUT

SOP

A

B

C

D

Y

0

0

0

0

1

0

0

0

1

1

0

0

1

0

1

0

0

1

1

1

0

1

0

0

0

-

0

1

0

1

1

0

1

1

0

1

0

1

1

1

1

1

0

0

0

0

-

1

0

0

1

0

-

1

0

1

0

0

-

1

0

1

1

0

-

1

1

0

0

1

1

1

0

1

1

1

1

1

0

0

-

1

1

1

1

0

-

จากนั้นนำทั้ง 4 เทอมมาทำการ OR กัน ก็จะได้ฟังก์ชันแบบ SOP ดังนี้

คลิกที่นี่ดูวงจร

จากนั้นทำการลดรูป ฟังก์ชันได้ดังนี้ คลิกที่นี้ดูการลดรูป

จะได้คำตอบดังนี้ คลิกที่นี่ดูวงจร

---

กลับ

ตัวอย่าง ที่ 4

Y(A,B,C,D)=(6,7,8,9,13,14,15) แปลงเป็นตารางจะได้ดังนี้

INPUT

OUTPUT

SOP

A

B

C

D

Y

0

0

0

0

0

-

0

0

0

1

0

-

0

0

1

0

0

-

0

0

1

1

0

-

0

1

0

0

0

-

0

1

0

1

0

-

0

1

1

0

1

0

1

1

1

1

1

0

0

0

1

1

0

0

1

1

1

0

1

0

0

-

1

0

1

1

0

-

1

1

0

0

0

-

1

1

0

1

1

1

1

1

0

1

1

1

1

1

1

จากนั้นนำทั้ง 4 เทอมมาทำการ OR กัน ก็จะได้ฟังก์ชันแบบ SOP ดังนี้

คลิกที่นี่ดูวงจร

จากนั้นทำการลดรูป ฟังก์ชันได้ดังนี้ คลิกที่นี้ดูการลดรูป

จะได้คำตอบดังนี้ คลิกที่นี่ดูวงจร

---

กลับ

ตัวอย่าง ที่ 5

จงลดรูปฟังก์ชันต่อไป นี้ f(A,B)=(2,3) โดยใช้ผังคาร์นอร์ ?

วิธีทำ
1. นำเอาสมการ f(A,B)=(2,3) แทนลง ในผังคาร์นอร์ ดังรูป

2. รวมช่องที่ติดกันเข้าด้วยกัน ในที่นี้เราสามารถรวมระหว่าง 2 และ 3 ได้ ดังรูป

3. จะได้คำตอบที่ลดรูปดังนี้

---

กลับ

ตัวอย่าง ที่ 6

จงลดรูปฟังก์ชันต่อไป นี้ f(A,B)=(0,3) โดยใช้ผังคาร์นอร์ ?

วิธีทำ
1. นำเอาสมการ f(A,B)=(2,3) แทนลง ในผังคาร์นอร์ ดังรูป

2. รวมช่องที่ติดกันเข้าด้วยกัน ในที่นี้เราสามารถรวมระหว่าง 2 และ 3 ได้ ดังรูป

3. จะได้คำตอบที่ลดรูปดังนี้

---

กลับ

ตัวอย่าง ที่ 7

จงลดรูปฟังก์ชันต่อไปนี้ f(A,B,C)=(0,2,5,7) โดย ใช้ผังคาร์นอร์

วิธีทำ
1. นำเอาสมการ f(A,B,C)=(0,2,5,7) แทน ลงในผังคาร์นอร์ ดังรูป
2. รวมช่องที่ติดกันเข้าด้วยกัน ในที่นี้เราสามารถรวมระหว่าง (0,2) และ (5,7) ได้ ดังรูป
3. จะได้คำตอบที่ลดรูปดังนี้

---

กลับ

ตัวอย่าง ที่ 8

จงลดรูปฟังก์ชันต่อไปนี้ f(A,B,C)=(2,3,4,5) โดย ใช้ผังคาร์นอร์

วิธีทำ
1. นำเอาสมการ f(A,B,C)=(2,3,4,5) แทน ลงในผังคาร์นอร์ ดังรูป
2. รวมช่องที่ติดกันเข้าด้วยกัน ในที่นี้เราสามารถรวมระหว่าง (2,3) และ (4,5) ได้ ดังรูป
3. จะได้คำตอบที่ลดรูปดังนี้

---

กลับ

ตัวอย่าง ที่ 9

จงลดรูปฟังก์ชันต่อไปนี้ f(A,B,C)=(0,1,4,5) โดย ใช้ผังคาร์นอร์

วิธีทำ
1. นำเอาสมการ f(A,B,C)=(0,1,4,5) แทน ลงในผังคาร์นอร์ ดังรูป
2. รวมช่องที่ติดกันเข้าด้วยกัน ในที่นี้เราสามารถรวมระหว่าง (0,1,4,5) เข้าด้วยกันทั้ง 4 เทอมเพียงครั้งเดียวได้ เพราะลักษณะการทำงานของผังคา ร์นอร์จะเป็นทรงกระบอก หรือ ทรงกลม ฉะนั้นเราจึงม้วนเข้าหากันได้ ดังรูป
3. จะได้คำตอบที่ลดรูปดังนี้

---

กลับ

ตัวอย่าง ที่ 10

จงลดรูปฟังก์ชันต่อไปนี้ f(A,B,C)=(0,5) โดยใช้ ผังคาร์นอร์

วิธีทำ
1. นำเอาสมการ f(A,B,C)=(0,5) แทน ลงในผังคาร์นอร์ ดังรูป
2. รวมช่องที่ติดกันเข้าด้วยกัน ในที่นี้เราไม่สามารถรวมได้เพราะเทอมทั้ง 2 อยู่ทะแยงมุมกัน ไม่เป็นไปตามกฏ ดังนั้นจึงไม่สามารถลดรูปฟังก์ชันได้เราจึงทำการตอบได้ทันที ดังรูป
3. จะได้คำตอบที่ลดรูปดังนี้

---

กลับ

ตัวอย่าง ที่ 11

จงลดรูปฟังก์ชันต่อไปนี้ f(A,B,C)=(1,5) โดยใช้ ผังคาร์นอร์

วิธีทำ
1. นำเอาสมการ f(A,B,C)=(1,5) แทน ลงในผังคาร์นอร์ ดังรูป
2. รวมช่องที่ติดกันเข้าด้วยกัน ในที่นี้เราสามารถรวมระหว่าง (1,5) เข้าด้วยกันได้ ทั้งนี้เพราะผังคา ร์นอร์เป็นรูปทรงกระบอกนั้นเอง ดังรูป
3. จะได้คำตอบที่ลดรูปดังนี้

---

กลับ

ตัวอย่าง ที่ 12

จงลดรูปฟังก์ชันต่อไปนี้ f(A,B,C)=(2,3,6,7) โดย ใช้ผังคาร์นอร์

วิธีทำ
1. นำเอาสมการ f(A,B,C)=(2,3,6,7) แทน ลงในผังคาร์นอร์ ดังรูป
2. รวมช่องที่ติดกันเข้าด้วยกัน ในที่นี้เราสามารถรวมระหว่าง (2,3,6,7) เข้าด้วยกันเพียงครั้งเดียว เพราะเทอมทั้ง 4 อยู่ติดกัน และเป็นไปตามกฏ โดยเราจะเลือกรวมทั่ง 4 เทอม หรือ ครั้งละ 2 เทอมก็ได้ แต่ถ้าเรารวมครั้งละ 2 เทอม เราจะต้องทำการลดรูปลงไปอีกได้ โดยใช้ทฤษฎีบูลีน ฉะนั้นถ้ารวมทั้ง 4 เทอมเราจะกระทำเพียงครั้งเดียวก็ได้ ดังรูป
3. จะได้คำตอบที่ลดรูปดังนี้

---

กลับ

ตัวอย่าง ที่ 13

จงลดรูปฟังก์ชันต่อไปนี้ f(A,B,C)=(1,3,5,7) โดย ใช้ผังคาร์นอร์

วิธีทำ
1. นำเอาสมการ f(A,B,C)=(1,3,5,7) แทน ลงในผังคาร์นอร์ ดังรูป
2. รวมช่องที่ติดกันเข้าด้วยกัน ในที่นี้เราสามารถรวมระหว่าง (1,2,5,7) ดูรายละเอียดกับตัวอย่างที่ 12 และจะได้ ดังนี้
3. จะได้คำตอบที่ลดรูปดังนี้