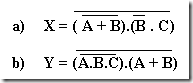5.2 พื้นฐานของพีชคณิตบูลลีน
ในพิชคณิตที่เรารู้จักกันจะแสดงค่าด้วยจำนวนเลข อาจอยู่ในรูปของเลขจำนวนเต็ม เศษส่วน จำนวนลบ สแควร์รูท ฯลฯ ประกอบกันเป็นสมาการ ตัวอย่างเช่น 10+(20 ÷ 5) x 2 = 28 แต่สำหรับพิชคณิตบูลลีน จะแสดงค่าด้วยสัญญลักษณ์ ที่เป็นสมการเช่นเดียวกัน แต่ค่าเหล่านั้นจะมีเพียง 2 ค่า คือ "จริง (True)" และ "เท็จ (False)" เท่านั้น ให้พิจารณาจากตัวอย่างข้างล่างนี้
ประโยค
ผลลัพธ์
ก. 10 เป็นจำนวนคี่
เท็จ (False)
ข. ดวง อาทิตย์มีแสงสว่างในตัวเอง
จริง (True)
ค. เดือน กันยายนมี 30 วัน
จริง (True)
ง. หนึ่ง สัปดาห์มี 5 วัน
เท็จ (False)
พีชคณิตบูลลีน จะเหมือนกับทฤษฎีของสวิตชิ่ง ซึ่งสวิตช์แต่ละอันจะมี เปิด (Open) และปิด(Close) ในดิจิตอลคอมพิวเตอร์ก็เช่นเดียวกัน วงจรลอจิกและหน่วยความจำซึ่งเป็นส่วนประกอบที่สำคัญ ก็มีค่าเป็นไปได้เพียงสองค่า คือ ค่า "0" และ "1" เราจะเรียกมันว่า Logoc 0 และ Logic 1 และสามารถที่จะแสดงได้หลายอย่างดังตารางข้างล่างนี้
LOGIC 0
LOGIC 1
เท็จ (False)
จริง (True)
Low
High
Off
On
No
Yes
Open Switch
Close Switch
แทนด้วยแรงดัน 0 - 0.8 V
แทนด้วยแรงดัน 2 - 5 V
.2.1 กระบวนการพื้นฐานทางตรรกะ (Logic Operation)
ตัวกระทำ (Operator)ที่ทำให้เกิดกระบวนการทางตรรกะมี 3 อย่างคือ AND OR และ NOT ซึ่ง จะได้อธิบายตามลำดับ ดังต่อไปนี้
ตัวกระทำ AND (AND operation) :
ตัวแปรและค่าคงที่ในวงจรลอจิก จะมีค่าได้เพียงสองค่า คือ false และ true หรือ 0 และ 1 ดังได้กล่าวมาแล้ว ซึ่งตัวแปรแต่ละตัวสามารถที่จะมารวม หรือจัดหมู่ (Combinations) กันให้อยู่ในรูปของนิพจน์ของพิชคณิตบูลลีน ด้วยตัวกระทำ AND OR และ NOT ถ้าตัวแปรทั้งสอง ถูกกระทำด้วยตัวกระทำ AND และตัวแปรทั้งสองมีค่าเป็นจริง (True) ผลลัพธ์ที่ได้ก็เป็น จริง (True) ตัวอย่าง เช่น
ประโยค
ผลลัพธ์
น้ำมีจุดเยือกแข็งที่ 0 องศาเซ็นเซียส AND น้ำมีจุดเดือดที่ 100 องศาเซ็นเซียส
จริง (True)
ดวงอาทิตย์ร้อน AND ดวงอาทิตย์ให้แสงสว่างในเวลากลางคืน
เท็จ(False)
การใช้ AND เป็นตัวกระทำระหว่างตัวแปร ทั้งสอง อาจเรียกว่า การคูณทางลอจิก (Logic Product หรือ Conjunction) โดยใช้สัญญลักษณ์ จุด (.) เป็น เครื่องหมายแทนการกระทำของตัวกระทำ AND เช่น A.B (อ่านว่า A and B) บางที่อาจเขียนโดยละสัญญลักษณ์ จุด เช่น AB (อ่านว่า A and B) ก็ได้
ตัวกระทำ OR (OR operation) :
ตัวกระทำ OR เมื่อกระทำกับ ตัวแปรสองตัว จะเป็นจริงเเมื่อ ตัวแปรทั้งสองมีค่าเป็นจริง และ ตัวแปรมีค่าเป็นจริงเพียงหนึ่งตัว ตัวอย่างเช่น
ประโยค
ผลลัพธ์
น้ำมีจุดเยือกแข็งที่ 0 องศาเซ็นเซียส ORน้ำมีจุดเดือดที่ 100 องศาเซ็นเซียส
จริง (True)
ดวงอาทิตย์ร้อน OR ดวงอาทิตย์ให้แสงสว่างในเวลากลางคืน
จริง (True)
ดวงจันทร์ขึ้นตอนกลางวัน OR ดวงอาทิตย์ขึ้นตอนกลางคืน
เท็จ(False
การใช้ตัวกระทำ OR อาจเรียกว่าเป็น การรวม ทางลอจิก (Logic Sum) ใช้สัญญลักษณ์ บวก (+) เป็นเครื่อง เช่น A + B (อ่านว่า A or B)
ตัวกระทำ NOT (NOT operation) :
ตัวกระทำ NOT เมื่อกระทำกับ ตัวแปรที่มีค่าเป็นจริง (True) ตัวแปรนั้นจะมีค่า เป็นตรงกันข้าม คือเป็น เท็จ (False) เช่น " 10 เป็นเลขจำนวนคี่" มีค่าเป็นเท็จ เมื่อมีตัวกระทำ NOT มากระทำ จะได้ "10 ไม่ใช่เลขจำนวนคี่" จะได้ค่าลอจิกเป็นจริง ใช้สัญญลักษณ์ Bar (— ) หรือ Dash (') เช่น 
หรือ A' (อ่านว่า NOT A)
4.2.2 บูลลีนฟังชั่นและนิพจน์ของบูลลีน (Boolean Function & Expression)
การนำตัวแปรหลายตัวมาจัดหมู่ (Conbination) หรือมากระทำด้วยตัวกระทำ AND, OR และ NOT จะเขียนให้อยู่ในรูปของ บูลลีนฟั่งชั่น หรืออาจเรียกว่า สวิทชิ่งฟังชั่น ได้ดังนี้ :-
f (A,B)
= 
f (A,B,C)
= 
การเขียนอาจจะเขียนได้อีกรูปแบบหนึ่ง (นิพจน์ของบูลลีน) ดังนี้
X
= ![image002[1]](http://lh3.ggpht.com/_Gp40BGpSBRk/S9BUj7tTVcI/AAAAAAAAA2U/wTyfapeqduo/s1600-h/image002%5B1%5D%5B2%5D.gif "image002[1]"){kind=small}
Y
= ![image003[1]](http://lh6.ggpht.com/_Gp40BGpSBRk/S9BUlLsV_AI/AAAAAAAAA2c/Zxs-Kx3Rg_E/s1600-h/image003%5B1%5D%5B2%5D.gif "image003[1]"){kind=small}
X และ Y แทนผลลัพธ์ (Output) ของฟังชั่นซึ่งอาจเป็นจริงหรือเท็จ (0 หรือ 1) ก็ได้ จะเห็นว่ารูปแบบดังกล่าว เป็นแบบของสมการทางคณิตศาสตร์ ซึ่งเรียกว่า นิพจน์ของบูลลีน
4.2.3 ตารางความจริงและไดอะแกรมแสดงเวลา (Truth Table & Timing Diagram)
ตัวแปรแต่ละตัวในบูลลีนฟังชั่นหรือนิพจน์ของบูลลี น จะมีค่าทางตรรกะได้ 2 ค่า คือ เท็จ (F) และ จริง (T) เมื่อนำตัวแปรมาจัดหมู่ หรือมากระทำต่อกัน ด้วยตัวกระทำ จำทำให้มีสถานะแตกต่างกันได้ เท่ากับ 2 ยกกำลัง n (n = จำนวนตัวแปร) เช่น f (A,B) มีตัว 2 ตัว สถานะความแตกต่าง คือ 2n = 22 = 4 ส่วน A,B นั้นเป็นตัวแปร เราจะเรียกว่า ตัวป้อนเข้า (Input) เมื่อถูกกระทำ จากตัวกระทำ (AND, OR, NOT) ก็จะให้ผลลัพธ์ (Output) ออกมา
เพื่อให้การออกแบบวงจรลอจิก หรือการวิเคราะห์วงจรทำได้ง่ายขึ้น เราจึงเขียนสถานะที่เป็นไปได้ของ อินพุตและ เอาท์พุต ออกมาในรูปของตาราง ซึ่งเรียกว่า ตารางความจริง (Truth Table) ดังตัวอย่างข้างล่างนี้ :-
Input
Output
A
B
X
F
F
T
F
T
F
T
F
F
T
T
T
จากตาราง ความจริง จะเขียนเป็น นิพจน์ของบูลลีน ได้ดังนี้ :- 
Input
Output
A
B
X
0
0
1
0
1
0
1
0
0
1
1
1
a) Truth table
b) Truth table
พิจารณาตารางความจริงข้างบน จะเห็นว่า Output (X) จะเป็นจริง (T หรือ 1)ได้ เมื่อ Input A และ B เป็นจริงหรือ A และ B เป็นเท็จทั้งคู่ (A และ B มีค่าทางลอจิก เหมือนกัน) ถ้าให้จริง (T) คือ "1" และเท็จ(F) คือ "0" จะเขียนตารางความจริง ได้ดังตาราง b
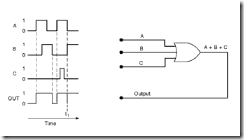
ในบางครั้งการออกแบบวงจรลอจิก หรือการวิเคราะห์วงจรอาจทำได้โดยเครื่องมืออีกอย่างหนึ่ง ซึ่งเรียกว่า ไดอะแกรม เวลา (Timimng diagram) เขียนโดยยึดหลัก เดียวกัน ดังตัวอย่างข้างล่างนี้ :-
ไดอะแกรมเวลา (Timimng diagram)
แกนนอนจะเป็นแกนแสดงเวลา (time) เริ่มต้นจาก t0, t1,t2,.. ไปเรื่อยๆ แต่ละช่วงเวลา จะแสดงสถานะของอินพุตและเอาท์พุตได้เช่นเดียวกันกับตารางความจริง ดังตารางข้างล่างนี้
ช่วงเวลา
input
output
B
A
X
t0 - t1
0
0
1
t1 - t2
0
1
0
t2 - t3
1
0
0
t3 - t4
1
1
1
ตัวอย่าง : จงเขียนตารางความจริง จาก สวิตชิ่งฟังชั่นหรือบูลลีนฟังชั่น ต่อไปนี้
พิจารณาจากบูลลีนฟังชั่นข้างบน จะได้
1. สถานะความเป็นไปได้ของอินพุตและเอาท์พุต 2n = 23 = 8
2. เอาท์พุตจะเป็น "1" เมื่อ เทอมใดเทอมหนึ่งหรือหลายเทอมมีค่าลอจิกเป็น "1"
(เพราะทุกเทอมถูกกระทำด้วยตัวกระทำ OR )
จะได้ตารางความจริงดังนี้ :-
Input
Output
A
B
C
f(A,B,C)
0
0
0
1
0
0
1
0
0
1
0
1
0
1
1
0
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
0
ตัวอย่าง : จากตารางความจริงจง เขียนสวิตชิ่งฟังชั่นหรือบูลลีนฟังชั่น f(A,B,C) = X
(ให้พิจารณาเฉพาะเทอมที่เป็น "1")
Input
Output
หมายเหตุ
A
B
C
X
0
0
0
0
0
0
1
1
*a
0
1
0
1
*b
0
1
1
0
1
0
0
1
*c
1
0
1
0
1
1
0
0
1
1
1
1
*d
a. X = 1 เมื่อ A=0 AND B=0 AND C=1 หรือ 
= 1
b. X = 1 เมื่อ A=0 AND B=1 AND C=0 หรือ 
= 1
c. X = 1 เมื่อ A=1 AND B=0 AND C=0 หรือ 
= 1
d. X = 1 เมื่อ A=1 AND B=1 AND C=1 หรือ ABC = 1
ดังนั้น 
5.3 เกตพื้นฐาน (Basic Logic Gates)
ในทางปฏิบัติอุปกรณ์ที่ใช้แทนตัวกระทำทางตรรกะ เราเรียกว่า เกต (Gate) ซึ่งประกอบ ขึ้นด้วยวงจรอิเล็กทรอนิกส์ โดยมีความคิดพื้นฐานมาจากวงจรสวิตชิ่ง สำหรับเกตพื้นฐานมี 3 ชนิด ได้แก่ AND , OR และ NOT นิพจน์บูลลีน หรือ ลอจิกฟังชั่น ส่วนใหญ่จะประกอบขึ้นด้วยเกตทั้งสาม จะขอกล่าวรายละเอียดของเกตแต่ละชนิดเกี่ยวกับ สัญญลักษณ์(logic symbol ) ตารางความจริง (Truth table ) ไดอะแกรมของเวลา (Timing diagram ) และนิพจน์บูลลีน (Boolean expression. )
แอนด์เกต (AND gate)
แอนด์เกต (AND gate) เป็นเกตที่มีอินพุตตั้งแต่สองอินพุตขึ้นไป เอาท์พุตของแอนด์เกตจะเป็น "1" ถ้า อินพุตทั้งหมดเป็น "1" ถ้ามีอินพุตใดอินพุตหนึ่ง เป็น "0" เอาท์พุตก็จะเป็น "0" ตาม ไปด้วย
สัญญลักษณ์ของ แอนด์เกต
วงจรไฟฟ้าเปรียบเทียบ
ข้างบนเป็นวงจรไฟฟ้าสำหรับเปรียบเทียบการทำงานของ แอนด์เกต โดยมี สวิตช์ A และ B ต่ออนุกรมกัน
- A เป็น สวิตช์ที่เทียบได้กับอินพุท A ของแอนด์เกต
- B เป็น สวิตช์ที่เทียบได้กับอินพุท B ของแอนด์เกต
- กำหนดให้ เมื่อสวิตช์ต่อวงจร (Close) มีค่าลอจิกเป็น "1" และเมื่อสวิตช์เปิดวงจร (Open) มีค่า ลอจิกเป็น "0"
- มีหลอดไฟมัน จะแสดงผลออกมาว่า สว่าง ("1") หรือดับ ("0")
- ถ้าสวิตช์ ทั้งสองต่อวงจร (Close) คือทั้งสองมีค่าลอจิกเป็น "1" จะทำให้หลอดไฟสว่าง ("1")
- ถ้าสวิตช์ ตัวหนึ่งตัวใดหรือทั้งสองตัวเปิดวงจร (Open) คือมีค่าลอจิกเป็น "0" จะทำให้หลอดไฟดับ ("0")
Input
Output
A
B
X
0
0
0
0
1
0
1
0
0
1
1
1
ตารางความจริง (Truth table )
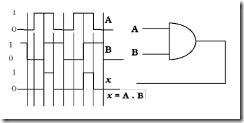
ไดอะแกรมของเวลา (Timing diagram )
f(A,B) = A.B หรือ X = A.B
นิพจน์บูลลีน (Boolean expression. )
ออร์เกต (OR gate)
ออร์เกต (OR gate) เป็นเกตที่มีอินพุตตั้งแต่สองอินพุตขึ้นไป เอาท์พุตของแอนด์เกตจะเป็น "1" ถ้า อินพุตหนึ่งอินพุทใดหรือทั้งสองมีระดับลอจิก เป็น "1" แต่ถ้าอินพุตทั้งสองเป็น "0" เอาท์พุตก็ จะเป็น "0" ด้วย
สัญญลักษณ์ของ ออร์เกต
ข้างบนเป็นวงจรไฟฟ้าสำหรับเปรียบเทียบการทำงานของ ออร์เกต โดยมี สวิตช์ A และ B ต่อขนานกัน
- กำหนดให้ เมื่อสวิตช์ต่อวงจร (Close) มีค่าลอจิกเป็น "1" และเมื่อสวิตช์เปิดวงจร (Open) มีค่า ลอจิกเป็น "0"
- มีหลอดไฟมัน จะแสดงผลออกมาว่า สว่าง ("1") หรือดับ ("0")
- ถ้าสวิตช์ ตัวหนึ่งตัวใดหรือทั้งสองตัวต่อวงจร (Close) คือมีค่าลอจิกเป็น "1" จะทำให้หลอดไฟสว่าง ("1")
- ถ้าสวิตช์ ทั้งสองตัวเปิดวงจร (Open) คือมีค่าลอจิกเป็น "0" จะทำให้หลอดไฟดับ ("0")
Input
Output
A
B
X
0
0
0
0
1
1
1
0
1
1
1
1
ตารางความจริง (Truth table ) ของออร์เกต 2 อินพุท 
ไดอะแกรมของเวลา (Timing diagram ) ออร์เกต 2 อินพุต 
ไดอะแกรม ของเวลา (Timing diagram ) ออร์เกต 3 อินพุต
f(A,B) = A+B หรือ X = A+B
f(A,B,C) = A+B+C หรือ X = A+B+C
นิพจน์บูลลีน (Boolean expression. )
น๊อตเกต (NOT gate)
น๊อตเกต (NOT gate) เป็นเกตที่มีอินพุตเพียงอันเดียว ดังรูปสัญญลักษณ์ที่แสดงข้างล่างนี้
สัญญลักษณ์ของ น๊อตเกต
อินพุตของ น๊อตเกต จะมีค่าลอจิกตรงกันข้าม (inverted ) กับ ทางเอาท์พุต ถ้าให้อินพุตมีค่าลอจิกเป็น "1" เอาท์พุตก็จะมีค่าลอจิกเป็น "0" แต่ถ้าให้อินพุตมีค่าลอจิกเป็น "0" ค่า ลอจิกทางเอาท์พุตก็จะเป็น "1"
![image001[1]](http://lh3.ggpht.com/_Gp40BGpSBRk/S9BU6bVprVI/AAAAAAAAA4U/8OJdE-iH42o/s1600-h/image001%5B1%5D%5B2%5D.gif "image001[1]"){kind=small}
อ่านว่า "NOT A" หรือ complement ของ 
.
Input
Outupt
![image021[1]](http://lh5.ggpht.com/_Gp40BGpSBRk/S9BU84JV_yI/AAAAAAAAA4k/QhsR1o24CxE/s1600-h/image021%5B1%5D%5B2%5D.gif "image021[1]"){kind=small}
X = 
0
1
1
0
ตารางความจริง (Truth table )
X = ![image001[2]](http://lh4.ggpht.com/_Gp40BGpSBRk/S9BVBp1FdTI/AAAAAAAAA5A/0AIGpCam9is/image001%5B2%5D_thumb.gif?imgmax=800 "image001[2]")
![image001[2]](http://lh3.ggpht.com/_Gp40BGpSBRk/S9BVA3ML44I/AAAAAAAAA48/ebc9H2_Tcas/s1600-h/image001%5B2%5D%5B2%5D.gif "image001[2]"){kind=small}
นิพจน์บูลลีน (Boolean expression. )
5.4 กฎของพีชคณิตบูลลีน
4.4.1 กฎพื้นฐานเกี่ยวกับทฤษฎีทางตรรกะ
ค่าทางลอจิกหรือ Logic Level มีได้เพียง 2 ค่า คือ "0" และ "1" เท่านั้น นั่นคือ
ถ้า A ไม่เท่ากับ "1"
นั่นคือ A = "0"
และ 
= "1"
ถ้า A ไม่เท่ากับ "0"
นั่นคือ A = "1"
และ ![image024[1]](http://lh3.ggpht.com/_Gp40BGpSBRk/S9BVDejpAxI/AAAAAAAAA5M/hdLPGaRnlX8/s1600-h/image024%5B1%5D%5B2%5D.gif "image024[1]"){kind=small}
= "0"
ตัวกระทำ OR
(การบวกทางลอจิก)
ตัวกระทำ OR
(การบวกทางลอจิก)
ตัวกระทำ NOT
(การ Complement หรือการกลับ ค่า)
0 + 0 = 0
0.0 = 0
= 1
0 + 1 = 1
0.1 = 0
= 0
1 + 0 = 1
1.0 = 0
1 + 1 = 1
1.0 = 1
4.4.2 ทฤษฎีพีชคณิตบูลลีนเกี่ยวกับตัวแปรหนึ่งตัว
จะขอแบ่งทฤษฎี พีชคณิตบูลลีนออกเป็นสองกลุ่มเพื่อสะดวกแก่การจดจำ คือ กลุ่มตัวแปรหนึ่งตัวและตัวแปรหลานตัว กลุ่มตัวแปรหนึ่วตัวมีดังนี้ :-
1
a) A.0 = 0
b) A+0 = 0
2
a) A.1 = A
b) A+1 = 1
3
a) A.A = A
b) A+A = A
4
a) A.![image024[2]](http://lh4.ggpht.com/_Gp40BGpSBRk/S9BVINgDx6I/AAAAAAAAA5k/tcIl3ZPCFwM/s1600-h/image024%5B2%5D%5B2%5D.gif "image024[2]"){kind=small}
= 0
b) A+![image024[3]](http://lh6.ggpht.com/_Gp40BGpSBRk/S9BVJblYIhI/AAAAAAAAA5s/qx_5_NOUByE/s1600-h/image024%5B3%5D%5B2%5D.gif "image024[3]"){kind=small}
=1
5
a) 
= A
4.4.3 ทฤษฎีพีชคณิตบูลลีนเกี่ยวกับตัวแปรหลายตัว
6
การสลับที่ (Commutative)
a) A+B = B+A
b) AB = BA
7
การจัดหมู่ (Associative)
a) A+(B+C) = (A+B)+C
b) A(BC) = (AB)C
8
การกระจาย (Distributive)
a) A(B+C) = AB + AC
b) A+BC = (A+B)(A+C)
9
การลดทอน (Absorption)
a) A+AB = A
b) A(A+B) = A
c) AB+A
= A
d) (A+B)(A+![image028[1]](http://lh4.ggpht.com/_Gp40BGpSBRk/S9BVOM0b8fI/AAAAAAAAA6E/XcYg7VhIe6c/s1600-h/image028%5B1%5D%5B2%5D.gif "image028[1]"){kind=small}
) =A
e) A+![image024[4]](http://lh3.ggpht.com/_Gp40BGpSBRk/S9BVPKV2IRI/AAAAAAAAA6M/FaCozVaemF4/s1600-h/image024%5B4%5D%5B2%5D.gif "image024[4]"){kind=small}
B = A+B
f) A(![image024[5]](http://lh5.ggpht.com/_Gp40BGpSBRk/S9BVQp6GHgI/AAAAAAAAA6U/eavZTDCSPMA/s1600-h/image024%5B5%5D%5B2%5D.gif "image024[5]"){kind=small}
+B) = AB
10
เดอมอร์แกน (DeMorgan's Law)
a) 
b) 
พิสูจน์ 8.b) A+BC = (A+B)(A+C)
A + BC
= (A+B)(A+C)
= AA+AC+AB+BC
......ผล จากการคูณวงเล็บ
= A + (AC+AB) + BC
......AA=A และจัดกลุ่มใหม่
= [A + A(C+B)] + BC
......ผล จากเอาตัวร่วม A ออก
= A + BC
......9.a) A+AB =A เมื่อมอง B คือ (B+C)
พิสูจน์ จากตารางความจริง
A
B
C
A+B
A+C
B.C
A+B.C
(A+B).(A+C)
0
0
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
1
0
1
0
0
0
0
0
1
1
1
1
1
1
1
1
0
0
1
1
0
1
1
1
0
1
1
1
0
1
1
1
1
0
1
1
0
1
1
1
1
1
1
1
1
1
1
จะ เห็นว่า 2 ช่อง ด้านขวามือ คือ A+B.C มีค่าระดับของลอจิกเท่ากับ (A+B).(A+C)
พิสูจน์ 9.a) A+AB = A
A + AB
= A.(1+B)
......เอา ตัวร่วม A ออก
= A.1
......1+B=1
= A
พิสูจน์ 9.b) A.(A+B) = A
A.(A + B)
= AA+AB
.....คูณ A เข้าในวงเล็บ
= A + AB
......A.A=A
= A.(1+B)
= A.1
= A
พิสูจน์จากตารางความจริง
A
B
A.B
A+B
A+AB
A.(A+B)
0
0
0
0
0
0
0
1
0
1
0
0
1
0
0
1
1
1
1
1
1
1
1
1
จะเห็นว่า 2 ช่อง ด้านขวามือ คือ A+A.B มีค่าระดับของลอจิกเท่ากับ A.(A+B)
4.4.2 ทฤษฎีของเดอมอร์แกน (DeMorgan's Law)
(a) ![image029[1]](http://lh5.ggpht.com/_Gp40BGpSBRk/S9BVUPmA3uI/AAAAAAAAA6s/cqtP8ZmwE58/s1600-h/image029%5B1%5D%5B2%5D.gif "image029[1]"){kind=small}
(b) ![image030[1]](http://lh6.ggpht.com/_Gp40BGpSBRk/S9BVVGPNkAI/AAAAAAAAA60/yibazTwWieE/s1600-h/image030%5B1%5D%5B2%5D.gif "image030[1]"){kind=small}
พิสูจน์ : ในข้อ (a). จะพิสูจน์ว่า 
เป็นคอมพลีเมนต์ (Complement) ของ (A+B) เมื่อเอา (A+B) มากลับ ค่าคือใส่ NOT ให้จะได้ 
ซึ่งจะมีค่าเท่ากับนิพจน์บูลลีนในข้อ (a).
กำหนดให้ y = (A+B)
ดังนั้น 
= ![image031[1]](http://lh3.ggpht.com/_Gp40BGpSBRk/S9BVZg5kyPI/AAAAAAAAA7U/_h9jd_u8G54/s1600-h/image031%5B1%5D%5B2%5D.gif "image031[1]"){kind=small}
เราต้องการจะพิสูจน์ว่า...
และ...
นิพจน์ ในข้อ (b) ก็สามารถพิสูจน์ได้ด้วยวิธี เดียว
.5 NAND/NOR Gates
NAND gate
แนนด์เกต (NAND gate) เป็นเกตที่มีอินพุตตั้งแต่สองอินพุตขึ้นไป เอาท์พุตของแอนด์เกตจะเป็น "0" ถ้า อินพุตทั้งหมดเป็น "1" ถ้ามีอินพุตเป็นอย่างอื่น เอาท์พุตก็จะเป็น "1" ทันที จะเห็นว่าเอาท์พุตจากแนนด์เกตจะเป็น NOT ของ A AND B หรือเป็น คอมพลีเมนต์ของ A.B นั่นเอง
ถ้านำเอา แอนด์เกต มาต่อเพิ่มด้วย น๊อตเกต ดังรูป ก็จะได้คุณสมบัติของแนนด์เกต และสามารถเขียน สัญญลักษณ์ได้ดังรูปถัดไป
ส่วน หัวของสัญญลักษณ์ ด้านเอาท์พุตจะทำเป็นวงกลม เรียกว่า invert bubble.
A
B
0
0
1
0
1
1
1
0
1
1
1
0
ตาราง ความจริงของ 2 อินพุตแนนด์เกต
เอาท์พุตจากแนนด์เกตคือ ![image038[1]](http://lh4.ggpht.com/_Gp40BGpSBRk/S9BVhDLLp1I/AAAAAAAAA8E/cPAUsNZ-IRY/s1600-h/image038%5B1%5D%5B2%5D.gif "image038[1]"){kind=small}
(อ่านว่า "A Nand B ") เขียนเป็นนิพจน์ บูลลีนได้ดังนี้
X = ![image038[2]](http://lh5.ggpht.com/_Gp40BGpSBRk/S9BViS6j4QI/AAAAAAAAA8M/dUSNW3oxor4/s1600-h/image038%5B2%5D%5B2%5D.gif "image038[2]"){kind=small}
NOR gate
นอร์เกต (NOR gate) เป็นเกตที่มีอินพุตตั้งแต่สองอินพุตขึ้นไป เอาท์พุตของนอร์เกตจะเป็น "1" ถ้า อินพุตทั้งหมดเป็น "0" ถ้ามีอินพุตเป็นอย่างอื่น เอาท์พุตก็จะเป็น "0" ทันที จะเห็นว่าเอาท์พุตจากนอร์เกตจะเป็น NOT ของ A OR B หรือเป็น คอมพลีเมนต์ของ![image032[1]](http://lh5.ggpht.com/_Gp40BGpSBRk/S9BVjTaTUzI/AAAAAAAAA8U/b6Acvlsirm8/s1600-h/image032%5B1%5D%5B2%5D.gif "image032[1]"){kind=small}
นั่นเอง
สัญ ญลักษณ์
A
B
X
0
0
1
0
1
0
1
0
0
1
1
0
ตารางความจริงของ 2 อินพุตนอร์แนนด์เกต
เอาท์พุต จากนอร์เกตคือ ![image032[2]](http://lh6.ggpht.com/_Gp40BGpSBRk/S9BVl-fi3GI/AAAAAAAAA8k/i9bZl80M6GQ/s1600-h/image032%5B2%5D%5B2%5D.gif "image032[2]"){kind=small}
(อ่านว่า "A NOR B ") เขียนเป็นนิพจน์ บูลลีนได้ดังนี้
X = ![image032[3]](http://lh5.ggpht.com/_Gp40BGpSBRk/S9BVnLCwreI/AAAAAAAAA8s/9caU6sH9uAo/s1600-h/image032%5B3%5D%5B2%5D.gif "image032[3]"){kind=small}
5.6 การใช้เกตทดแทน (Alternate Logic Gate)
1. การประยุกต์ NOR gate และ NAND gate
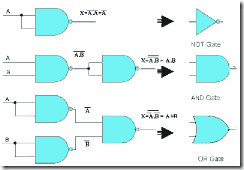
NAND Gate ประยุกต์เป็น NOT,AND และ OR Gate
OR Gate ประยุกต์เป็น NOT,AND และ OR Gate 
ตัวอย่าง จากวงจรลอจิกข้างล่าง จงเปลี่ยนทั้งหมดโดยใช้ NAND Gate แทน 
2. ทางเลือกในการใช้เกต
เก ตพื้นฐานและ NAND,NOR Gate สามารถ ประยุกต์ใช้แทนกันได้ ดังรูปสัญญลักษณ์ข้างล่างนี้ 
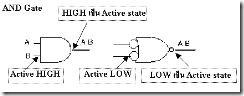
ในการใช้งานเกต จะมีลักษณะของระดับลอจิกอยู่สองอย่าง คือ HIGH Level และ LOW Level สถานะการทำงาน ของเกตเราจะเรียกว่า Active state สำหรับเกตที่มี สัญญาลักษณ์วงกลม (bubble) อยู่ไม่ว่าจะเป็นด้านอินพุตหรือ เอาท์พุตก็ตาม สถานะการทำงาน (Active state) จะเป็น Active LOW และถ้าไม่มีวงกลมสถานะการทำงานเราจะเรียกว่า Active HIGH ดังตัวอย่างข้างล่าง :-
NOR Gate
AND Gate
5.7 การเขียนวงจรลอจิกและนิพจน์ บูลลีน
4.7.1 การเขียนวงจรลอจิก
4.7.2 นิพจน์บูลลีนและการหาค่าระดับลอจิกเอาท์พุต
4.7.3 การวงจรลอจิกจากสมการลอจิกและเขียนสมการลอจิกจากวง จรลอจิก
5.8 เกตชนิดพิเศษ
4.7.1 eXclusive-OR Gate (XOR)
เอ็กซ์คลูซีฟนอร์เกต (XOR gate) เป็นเกตที่มีอินพุตตั้งแต่สองอินพุตขึ้นไป จะให้เอาท์พุตเป็นลอจิก 0 เมื่อ อินพุตมีลอจิกเหมือนกัน และเอาท์พุตจะเป็นลอจิก 1 เมื่อ อินพุตมีลอจิกต่างกัน โดยนำมากระทำกันครั้งละ 2 อินพุต ให้พิจารณาจาก XOR ชนิด 2 อินพุต และ 3 อินพุต จากตารางความจริงข้างล่าง
A
B
X
0
0
0
0
1
1
1
0
1
1
1
0
ตารางความจริง 2 อินพุต
วงจรไฟฟ้าที่เทียบเท่า
สัญญลักษณ์
นิพจน์บูลลีน (Bollean Expression) : X= 
เอาท์พุต จาก XOR gate คือ ![image049[1]](http://lh3.ggpht.com/_Gp40BGpSBRk/S9BV0dMxHqI/AAAAAAAAA98/0gKkMKrCuWU/s1600-h/image049%5B1%5D%5B2%5D.gif "image049[1]"){kind=small}
อ่านว่า "A XOR B".
วงจรของ XOR เกต จากเกตพื้นฐาน
จากตารางความจริงข้างบน จะเห็นว่าเอาท์พุตของ XOR คือ X = "1" เมื่อ :-
A = "0" และ B = "1" หรือ ![image024[6]](http://lh5.ggpht.com/_Gp40BGpSBRk/S9BV1rFa35I/AAAAAAAAA-E/kv0pVoKAfdg/s1600-h/image024%5B6%5D%5B2%5D.gif "image024[6]"){kind=small}
.B = "1"
หรือ
A = "1" และ B = "0" หรือ A.![image028[2]](http://lh4.ggpht.com/_Gp40BGpSBRk/S9BV2-WQe_I/AAAAAAAAA-M/0ssS_aJ0-bs/s1600-h/image028%5B2%5D%5B2%5D.gif "image028[2]"){kind=small}
= "1"
ดังนั้นจะได้สมการบูลลีน : X = A.![image028[3]](http://lh3.ggpht.com/_Gp40BGpSBRk/S9BV4xo_BpI/AAAAAAAAA-U/MB7mRrFMWmc/s1600-h/image028%5B3%5D%5B2%5D.gif "image028[3]"){kind=small}
+![image024[7]](http://lh6.ggpht.com/_Gp40BGpSBRk/S9BV6R5QFWI/AAAAAAAAA-c/sSWw54UoMs0/s1600-h/image024%5B7%5D%5B2%5D.gif "image024[7]"){kind=small}
.B = 
A
B
A.![image028[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhaasmqj6XsJOrtaedduvpWOqVNFAg3wrhm8ULYEl5zpNN6g-WFGsRpzffXsgQp3YcDQQzw5WGVg7rhcIaNYBF8T0zkDVxO4gvgaxJIx8ashR5Xps3OYRp6jvEXb0DCrzlDR_9BAFUpO6o/s1600-h/image028%5B4%5D%5B2%5D.gif "image028[4]"){kind=small}
![image024[8]](http://lh6.ggpht.com/_Gp40BGpSBRk/S9BV-eMMYGI/AAAAAAAAA-0/5bCSNWBphuY/s1600-h/image024%5B8%5D%5B2%5D.gif "image024[8]"){kind=small}
.B
X
0
0
0
0
0
0
1
0
1
1
1
0
1
0
1
1
1
0
0
0
ตารางความจริง
วงจรลอจิกจากเกตพื้นฐาน
A
B
C
0
0
0
0
0
1
0
1
1
0
0
1
1
1
0
0
0
0
1
1
0
1
1
0
1
0
1
0
1
1
1
1
ตารางความจริงของ XOR gate 3 อินพุต
นิพจน์ บูลลีน (Bollean Expression) : X= ![image052[1]](http://lh6.ggpht.com/_Gp40BGpSBRk/S9BWB_5eGMI/AAAAAAAAA_M/p0PGYRvu8AY/s1600-h/image052%5B1%5D%5B2%5D.gif "image052[1]"){kind=small}
4.7.2 eXclusive-NOR Gate (XNOR)
เอ็กซ์คลูซีฟนอร์เกต (XOR gate) เป็นเกตที่มีอินพุตตั้งแต่สองอินพุตขึ้นไป เอาท์พุตจะให้ผลตรงกันข้ามกับ XOR คือ จะให้เอาท์พุตเป็นลอจิก 1 เมื่อ อินพุตมีลอจิกเหมือนกัน และเอาท์พุตจะเป็นลอจิก 0 เมื่อ อินพุตมีลอจิกต่างกัน สำหรับสัญญลักษณ์ก็จะเหมือนกับ XOR แต่จะมีปุ่มกลม ( invert bubble ) อยู่ที่เอาท์พุต
A
B
X
0
0
1
0
1
0
1
0
0
1
1
1
ตารางความจริง 2 อินพุต
วงจรไฟฟ้าที่เทียบเท่า
สัญญลักษณ์
นิพจน์บูลลีน (Bollean Expression) : X= 
เอาท์พุตจาก XNOR gate คือ ![image056[1]](http://lh4.ggpht.com/_Gp40BGpSBRk/S9BWGwnw26I/AAAAAAAAA_s/gJYNMS3jfqg/s1600-h/image056%5B1%5D%5B2%5D.gif "image056[1]"){kind=small}
อ่านว่า "A XNOR B".
วงจรของ XNOR เกต จากเกตพื้นฐาน
จากตารางความจริงข้างบน จะเห็นว่าเอาท์พุตของ XNOR คือ X = "1" เมื่อ :-
A = "0" และ B = "0" หรือ ![image031[2]](http://lh6.ggpht.com/_Gp40BGpSBRk/S9BWICsBkJI/AAAAAAAAA_0/mHt5mbYgn08/s1600-h/image031%5B2%5D%5B2%5D.gif "image031[2]"){kind=small}
= "1"
หรือ
A = "1" และ B = "1" หรือ A.B = "1"
ดังนั้นจะได้สมการบูลลีน : X =![image031[3]](http://lh6.ggpht.com/_Gp40BGpSBRk/S9BWJUMQC0I/AAAAAAAAA_8/ogbJj8vkV8w/s1600-h/image031%5B3%5D%5B2%5D.gif "image031[3]"){kind=small}
+A.B = 
สร้างสมการ ของ XNOR จาก สมการของ XOR :-
เอาท์พุตของ XNOR จะเป็นคอมพลีเมนต์กับเอาท์พุตของ XOR ดังนั้นจะได้สมการลอจิกดังนี้
A
B
![image031[4]](http://lh6.ggpht.com/_Gp40BGpSBRk/S9BWNga3bkI/AAAAAAAABAU/zGb4jlAQygI/s1600-h/image031%5B4%5D%5B2%5D.gif "image031[4]"){kind=small}
A.B
X
0
0
1
0
1
0
1
0
0
0
1
0
0
0
0
1
1
0
1
1
ตารางความจริง
วงจรลอจิกจากเกตพื้นฐาน
A
B
C
0
0
0
1
0
1
0
0
1
0
0
0
1
1
0
1
0
0
1
0
0
1
1
1
1
0
1
1
1
1
1
0
ตารางความจริงของ XNOR gate 3 อินพุต
นิพจน์ บูลลีน (Bollean Expression) : X= ![image060[1]](http://lh3.ggpht.com/_Gp40BGpSBRk/S9BWR3fzV_I/AAAAAAAABAs/HNaa0Z8Xmbk/s1600-h/image060%5B1%5D%5B2%5D.gif "image060[1]"){kind=small}
4.7.3 การประยุกต์ใช้เกตพิเศษ
วงจรสร้างพาริตี้บิทและ วงจรตรวจสอบพาริตี้ (Parity Generator & Patrity Checker)
วงจรเปลี่ยน Gray code เป็น Binary และ Binary เป็น Gray code
แบบฝึกหัด
1. จากวงจรลอจิกข้างล่าง
a) จงสร้าง บูลลีนฟังชั่นของ A, B C และD
b) จากอินพุตที่กำหนดให้ จงพิจารณา แล้วใส่ค่าระดับลอจิกที่เอาท์พุตของเกตแต่ละตัว
2. จงเขียนวงจรลอจิกจากสมการลอจิกดังต่อไป นี้ 
3. ก. จงลดทอนสมการลอจิกโดยใช้พิชคณิตบูลลีน 
ข. จากข้อ 3 ก. จงเปลี่ยนผลลัพธ์ที่ได้ เป็น NAND Gate
4. จงเขียนวงจรลอจิกจากสมการ 
และสร้างตารางความจริงจากวงจร
5. จงใช้พีชคณิตบูลลีนพิสูจน์
a) ac + a'bc + = c(a + b)
b) (a + c).(a' + b + c) = ab + c
c) ab + a'c +bc = ab + a'c
6. จงเขียนวงจรลอจิกและตารางความจริง
a) X = a'b + ab'
b) Y = (a + b).(a b)'
7. จงใช้พิชคณิตบูลลีนพิสูจน์ ว่าสมการ ข้อ 6. a เท่า กับ ข้อ 6.b
8. จงเปลี่ยนวงจรเกตพื้นฐานของ XOR โดย ใช้ NAND Gate ทั้งหมด เขียนวงจร
